
- #FIND THE RABBIT AND FOX POPULATION AS A FUNCTION OF TIME CODE#
- #FIND THE RABBIT AND FOX POPULATION AS A FUNCTION OF TIME PLUS#
It says, terminate when y returns to the point where its angle mu is the same as the angle between eta and mu. But I want to look at this to see how the calculation is done. I'm going to- I have a display function in here. And when g returns to 0, the integration is stopped.
#FIND THE RABBIT AND FOX POPULATION AS A FUNCTION OF TIME CODE#
This code is called every time step in the integration.Īnd I'm not going to go into detail here, but it computes a function g that we're looking to see when this is 0. So I'm going to use ODE's set to provide an event handler called Pit Stop. In the MATLAB ODE suite, this is done with an event handler. Determining the period of a periodic solution is often the important part of a calculation. And we can see here, we've gone over three periods and return back to our initial values of 100 and 300.Īnd now I'm going to use something that'll show off the periodicity of function in MATLAB called Comet.
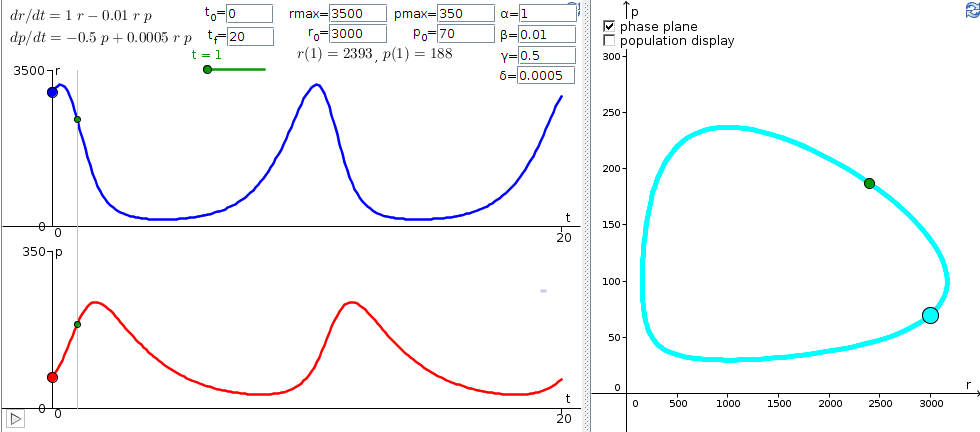
10 to the minus 6.Īnd let's capture the solution and integrate over three periods. And so I can- I'm going to set- I want to compute to higher accuracy. And we've integrated over something more than three periods. And it looks like the period, it's returning back to the initial condition is 100 and 400.Īnd it's returning back to that along about here. And then choose ODE 45 and we'll integrate from 0 to 25. OK, let's bring up MATLAB and compute a solution. But the period is greater than 2pi and the orbit is far from an ellipse. On the other hand, if the initial conditions are far from the critical point, then it turns out the solution is still periodic. If the initial conditions are close to the critical point, the solution is periodic. But we do know this about their behavior. We can't express the solution in terms of simple analytic functions. And so this critical point is a stable center with a period 2pi.
#FIND THE RABBIT AND FOX POPULATION AS A FUNCTION OF TIME PLUS#
The eigenvalues of the Jacobian are plus or minus I. And at the critical point, the Jacobian- here's the Jacobian. So that's the point where y1 and y2 are equal to the mu1 and mu2. There's a critical point at the origin.īut the interesting one is when these terms become 0. The critical points are when the derivatives become 0. These are, after all, models that are idealized versions of what's happening in nature.

We can have half of a rabbit or a tenth of a moose. Don't worry about the fact that these are continuous variables and that we can have non-integer numbers of individuals. So these four parameters, two mus and two etas, are the four parameters we have in our predator prey model. So we have two values eta 1 and eta 2, which are the initial values of y1 and y2. To complete this specification, we need the initial conditions. On the other hand, the decay of y2 becomes 0 when y1 reaches mu1. So y1 will grow until this term becomes 0 one y2 read reaches mu2. The growth of Y1 is limited by the presence of y2. These are like logistics terms, except with the interaction between the two species. And the predators die off exponentially in the absence of any prey.īut then here are the non-linear terms. So y2 prime equals minus y2 represents exponential decay. So in the absence of any prey, this minus sign is all important. The predators need the prey, live on the prey.

So y1 prime equals y1 represents exponential growth of the prey in the absence of any predators. I've chosen the units of time and population so that the coefficients in front of the leading linear terms are one. Y1 represents the prey, who would live peacefully by themselves if there were no predators. Think of the two species as rabbits and foxes or moose and wolves or little fish in big fish. They are the foundation of fields like mathematical ecology. The Lotka-Volterra predator prey equations are the granddaddy of all models involvement competition between species.


 0 kommentar(er)
0 kommentar(er)
